#11 삽입정렬(Insertion

● 삽입 정렬?

– 삽입정렬도 어렵지 않으나 성능이 떨어진다.

– 삽입정렬은 선택정렬과 동일합니다. 배열을 두 범위(정렬 및 비정렬)로 분할하다.

– 삽입 정렬은 정렬되지 않은 범위의 시작 부분에서 데이터를 하나씩 빼내고, 적절한 위치에 붙여넣기하여 정렬알고리즘오전.

(4, 1, 5, 3, 6, 2)

– 참고 삽입 정렬은 첫 번째 요소(인덱스 = 0)가 이미 정렬되어 있다는 가정하에 정렬하는 알고리즘입니다.오전.

– 아래 그림을 보면 (index(0) = 4)만 정렬되어 있다.

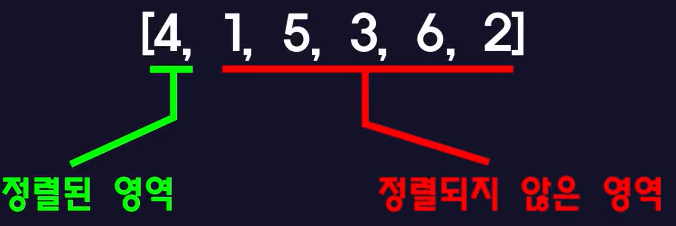
하나.

– 정렬되지 않은 범위의 첫 번째 요소(Index(1) = 1)를 정렬된 범위에 붙여넣습니다.

– 삽입할 요소(index(1) = 1)는 정렬된 범위의 마지막 요소(index(0) = 4)와 비교됩니다.

cf) 이제 정렬된 범위에 요소가 있으므로 (index(0) = 4)가 첫 번째이자 마지막 요소입니다.

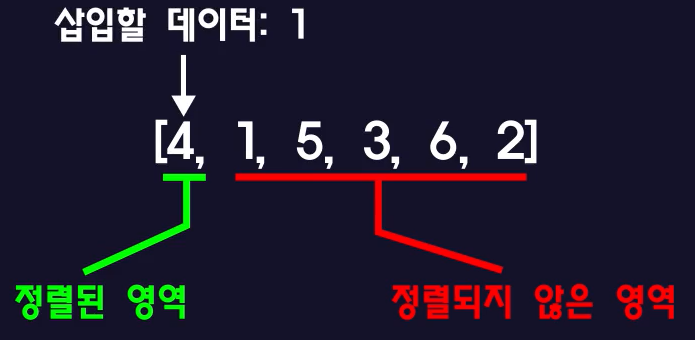
– (1 < 4) 그래서 4 오른쪽 인덱스(index(1))를 덮어씁니다.

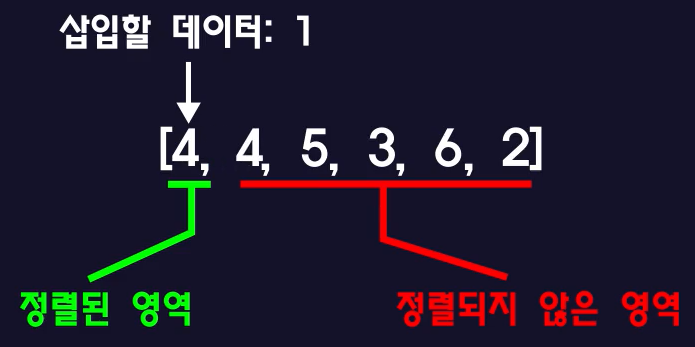
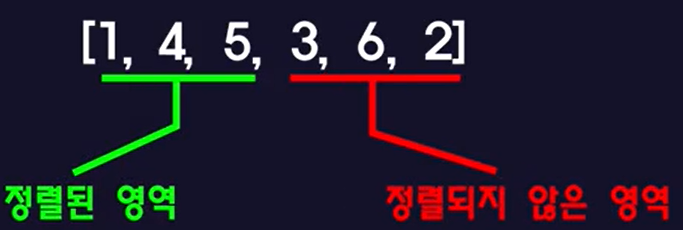
– 이제 삽입할 날짜 1을 정렬된 범위의 다른 요소와 비교해야 합니다. 더 이상 비교할 요소가 없으므로 날짜 1은 마지막 비교 위치인 ‘4’에 삽입됩니다.끼워 넣다’그렇습니다

– 이후 정렬된 영역과 정렬되지 않은 영역은 다음과 같습니다.

2.

– 정렬되지 않은 영역 첫 번째 요소(index(2) = 5)를 정렬된 범위에 삽입해 보겠습니다.

– 이를 위해 정렬된 범위의 마지막 요소부터 역순으로 비교하다.

– 현재 정렬된 범위 뒤에 있는 데이터는 (index(1) = 4)이므로 4와 5를 비교하고 있습니다.

– (4 < 5)는 (index(2) = 5)를 현재 위치에 유지하므로 올바르게 정렬되었음을 의미합니다.

– 후에 정렬된 영역과 정렬되지 않은 영역은 아래와 같습니다.

삼.

– 정렬되지 않은 영역 첫 번째 요소(index(3) = 3)를 정렬된 범위에 삽입해 보겠습니다.

– 이를 위해 정렬된 범위의 마지막 요소부터 역순으로 비교하다.

– 현재 정렬된 영역의 뒷면에 있는 데이터 (인덱스(2) = 5) 그래서 우리는 5와 3을 비교합니다.

– (3 < 5) 그래서 5 올바른 인덱스를 덮어씁니다.

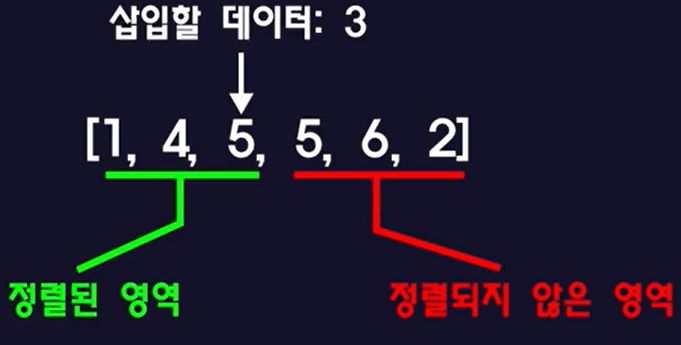
– 삽입할 데이터 3을 직전에 비교한 5의 이전 데이터(=4)와 비교하자.

– (3 < 4) 그래서 4붓다 올바른 인덱스를 덮어씁니다.

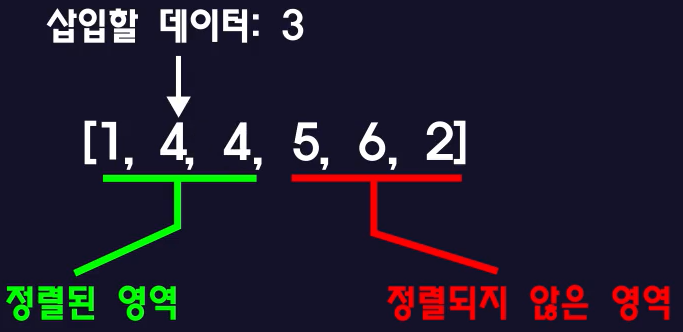
– 삽입할 데이터 3과 직전에 비교한 데이터 4의 이전 데이터(=1)를 비교해보자.

– 이후 (1 < 3) 가장 가까운 인덱스 1로 3을 덮어씁니다.

– 후에 정렬된 영역과 정렬되지 않은 영역은 아래와 같습니다.

– 이 과정을 반복하면 오름차순으로 정렬됩니다.

(1, 2, 3, 4, 5, 6)  -->  Insertion Sort이 끝난 모습

---

● 시행

– 삽입 정렬은 첫 번째 요소(인덱스 = 0)가 이미 정렬되어 있다는 가정하에 정렬하는 알고리즘입니다.오전.

function insertionSort(arr) {
    // 정렬되지 않은 영역의 (첫 번째 원소 ~ 마지막 원소)를 순회하기 위한 for문
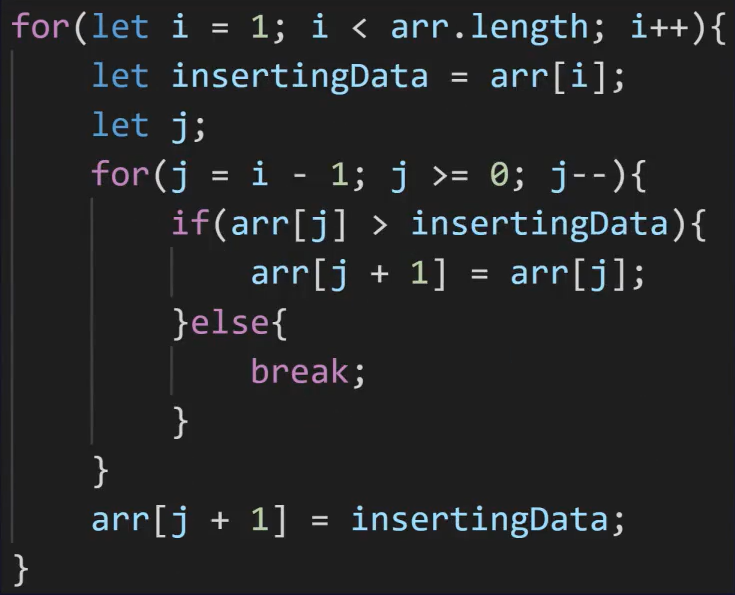
    for(let i = 1; i < arr.length; i++) {
        // 정렬 되지 않은 영역의 첫 번째 데이터(원소) = 삽입할 데이터
        let insertingData = arr(i);

        // 삽입 위치
        let j;

        // 정렬된 영역의 (맨 뒤 ~ 첫 번째 원소)를 역순으로 순회하며 삽입할 데이터의 위치를 찾는 for문
        for(j = (i - 1); j >= 0; j--) {
            if(arr(j) > insertingData) {
                // (현재 순회하는 인덱스의 원소 > insertingData)라면 순회하는 인덱스를 오른쪽 index에 덮어씌운다.
                arr(j + 1) = arr(j);
            } else {
                // insertingData 보다 작은 최초 원소를 발견했으니 for 문 종료
                // 그 이상은 비교해봤자 어차피 insertingData가 더 크다.
                // 삽입할 원소보다 작은 원소의 index는 현재 변수 j에 들어있는 상태이다.
                break;
            }
        }

        // j 보다 1 큰 위치에 insertingData 삽입
        arr(j + 1) = insertingData;
    }
}

let arr = (4, 1, 5, 3, 6, 2);

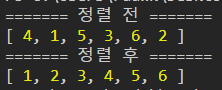
console.log("======= 정렬 전 =======");
console.log(arr);

insertionSort(arr);

console.log("======= 정렬 후 =======");
console.log(arr);

let i = 1
- Insertion Sort는 첫 번째 원소(index = 0)는 이미 정렬이 되어있다는 가정하에 정렬을 하는 알고리즘이므로
index(0) 원소는 굳이 순회할 필요없다.
- 반대로 말하면 (index = i)에 해당하는 원소는 아직 정렬이 되지 않은 영역의 첫 번째 데이터인 것이다.

let j = (i - 1)
- 정렬된 영역의 마지막 원소 = 정렬되지 않은 영역의 첫 번째 원소의 한 칸 앞
- 정렬되지 않은 영역의 첫 번째 원소는 i 이므로  j = (i - 1)로 선언해 정렬된 영역의 맨 뒤로 설정한다.

arr(j + 1) = insertingData;
- if(arr(j) > insertingData) --> 이 조건이 false가 된 것
- 즉, arr(j)의 바로 앞에 insertingData를 넣어야 한다는 의미이므로 +1 을 해줘야한다.

---

● 삽입 정렬 성능 및 장단점

– 삽입 정렬에는 거품 정렬 및 선택 정렬과 유사한 for 문도 있습니다.

– 다시 말해서, 삽입 정렬의 성능도 O(n^2) 오전.